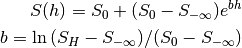5. Background and Calculations¶

5.1. Flow diagram of the program suite¶

$digraph foo { concentrate=true center=true fixedsize=true adnite2[shape=egg, label=<adnite2-gui>, color=blue, fontname="helvetica", penwidth=2] adnite2g[shape=egg, label=<adnite2-cli --graphics>, color=blue, style=bold, fontname="helvetica"] adnite2r[shape=egg, label=<adnite2-cli --rst>, color=blue, style=bold, fontname="helvetica"] rst2html[shape=egg, label=<rst2html>, color=blue, fontname="helvetica", penwidth=2] rst2pdf[shape=egg, label=<rst2pdf>, color=blue, fontname="helvetica", penwidth=2] conf[label="Cofiguration-\nFile", shape=parallelogram, fontname="helvetica", penwidth=2, color=black] input[label="GUI-Input", shape=parallelogram, fontname="helvetica", penwidth=2, color=red] loc[label="Location\nSqlite3-DB", shape=parallelogram, fontname="helvetica", penwidth=2, color=black] param[label=< Parameter File >, shape=parallelogram, style=bold, color=blue] png[label="png-\nimages", fontname="helvetica", shape=parallelogram, color=red, penwidth=2] rst[shape=box, label="rst-table", shape=parallelogram, color=blue, penwidth=2, fontname="helvetica"] pdf[label="pdf", fontname="helvetica", shape=parallelogram, color=red, penwidth=2] html[label="html", fontname="helvetica", shape=parallelogram, color=red, penwidth=2] conf -> adnite2; input -> adnite2; loc -> adnite2 adnite2 -> param; param -> adnite2g; param -> adnite2r; loc -> adnite2g; loc -> adnite2r; adnite2g -> png; adnite2r -> rst; png -> rst2html; rst -> rst2html; png -> rst2pdf; rst -> rst2pdf; rst2html -> html; rst2pdf -> pdf; }$

5.2. Astronomic caculations¶

Astronomic caculations were done with help of the pyephem library

To get the “right” night following the actual day all calculations are centered about mean local midnight (MLM):

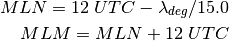
$MLN = 12\; UTC - \lambda_{deg} /15.0 MLM = MLN + 12\; UTC$

(MLN .. mean local noon).

5.2.1. Sunrise, sunset, moonrise, moonset¶

To render the results of the The United States Naval Observatory (USNO) [1] following procedure was applied according to Naval Observatory Rising and Settings

Observer at the height of the horizon (e.g. sea level)
Calculation is done for the upper limb of sun and moon
No air pressure $p_0 = 0$
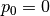
altitude of the horizon $h=-0°:34'$ (taking care of the mean apparent sun radius and for the average atmospheric refraction).

5.2.2. Twilight times¶

No air pressure $p_0 = 0$
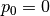
Calculation is done for the center of the sun.
Cicil Twilight: $h = -6°:00'$
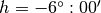
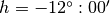
Nautical Twilight: $h = -12°:00'$
Astronomical Twilight: 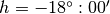$h = -18°:00'$ (not displayed in adnite)

5.2.3. Moon positions and phases¶

No atmosphere ( $p_0=0$ ) and no refraction
Phases are given in percent of the full moon disc

5.3. Illuminance caculation¶

The direct sun illuminance is not calculated. Only indirect sun illuminance during twilight and moon illuminance is calculated.

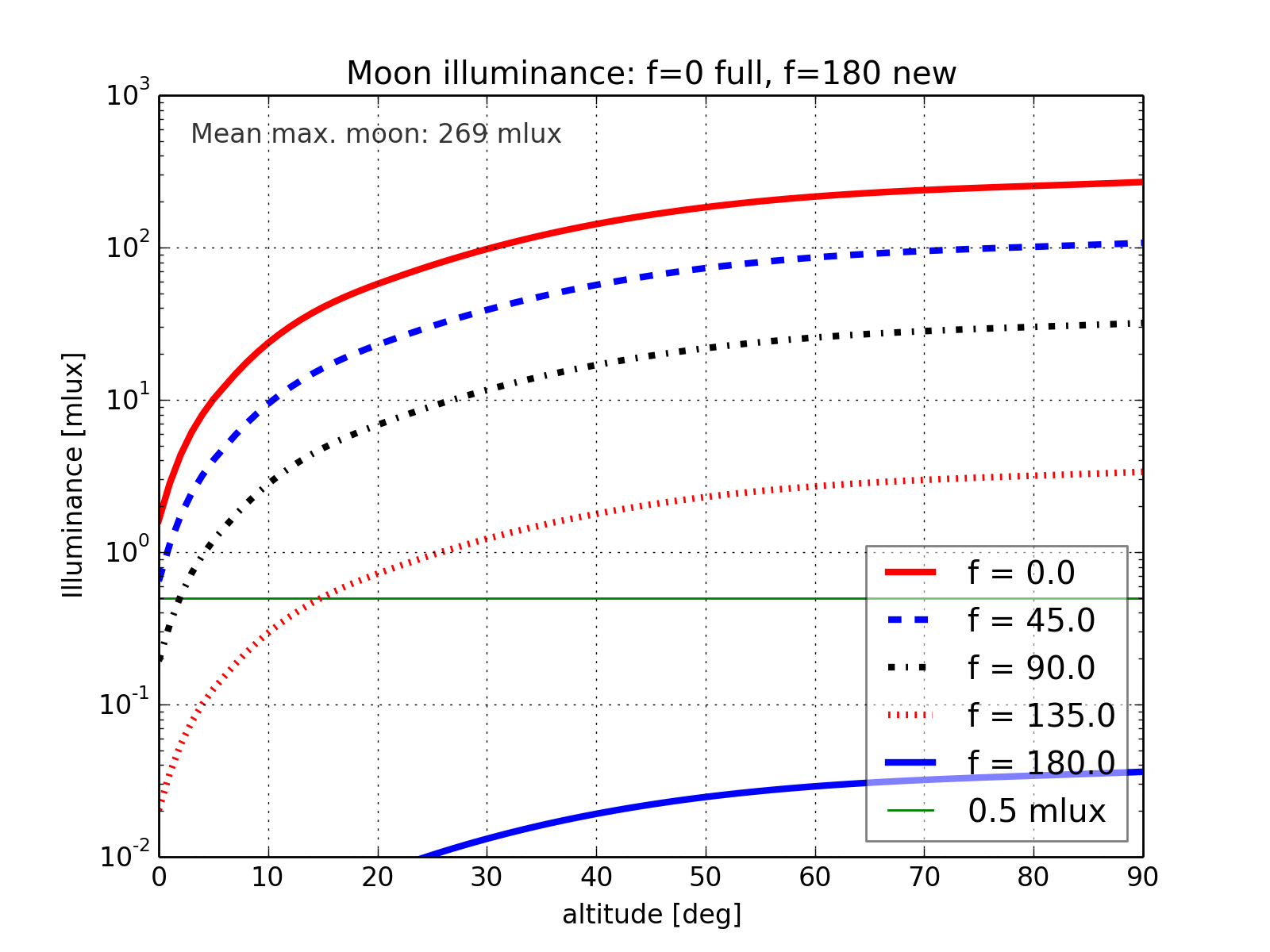
5.3.1. Moon illuminance at clear sky¶

It follows the empirical formula given in Urban, Seidelmann (2013), p. 518 ff.

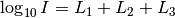
$\log_{10} I = L_1 + L_2 +L_3$

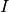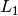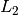with $I$ the ground illuminance in lux, $L_1$ for the ground illuminance of the full moon (at the mean distance) as function of altitude, $L_2$ the correction for moon phase and 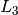$L_3$ the correction for the parallax.

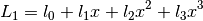
$L_1 = l_0 + l_1 x + l_2 x^2 + l_3 x^3$

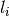with $x = h[deg]/90$ as the normalized moon altitude. The values for the $l_i$ are defined for different moon altitudes:

Alt. range [deg]	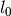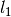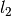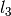$l_0$	$l_1$	$l_2$	$l_3$	Max error
20 - 90	-1.95	4.06	-4.24	1.56	0.02
5 - 20	-2.58	12.58	-42.58	59.06	0.03
-0.8 - 5	-2.79	24.27	-252.95	1321.29	0.03

The phase dependence is given by the negative definite expression

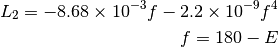
$L_2 = -8.68 \times 10^{-3} f - 2.2 \times 10^{-9} f^4 f = 180 - E$

and 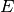$E$ is the elongation between sun and moon ( 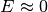$E \approx 0$ new moon, 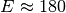$E \approx 180$ full moon).

The relative illuminous emittance of the moon depending on its phase.

The moon illuminance depending on height and phase.

Simplifications

neglecting varying sun-earth-moon distances that effect moon brightness
neglecting parallax effects 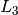$L_3$ between the topographic position on earth and the center line between moon and earth.

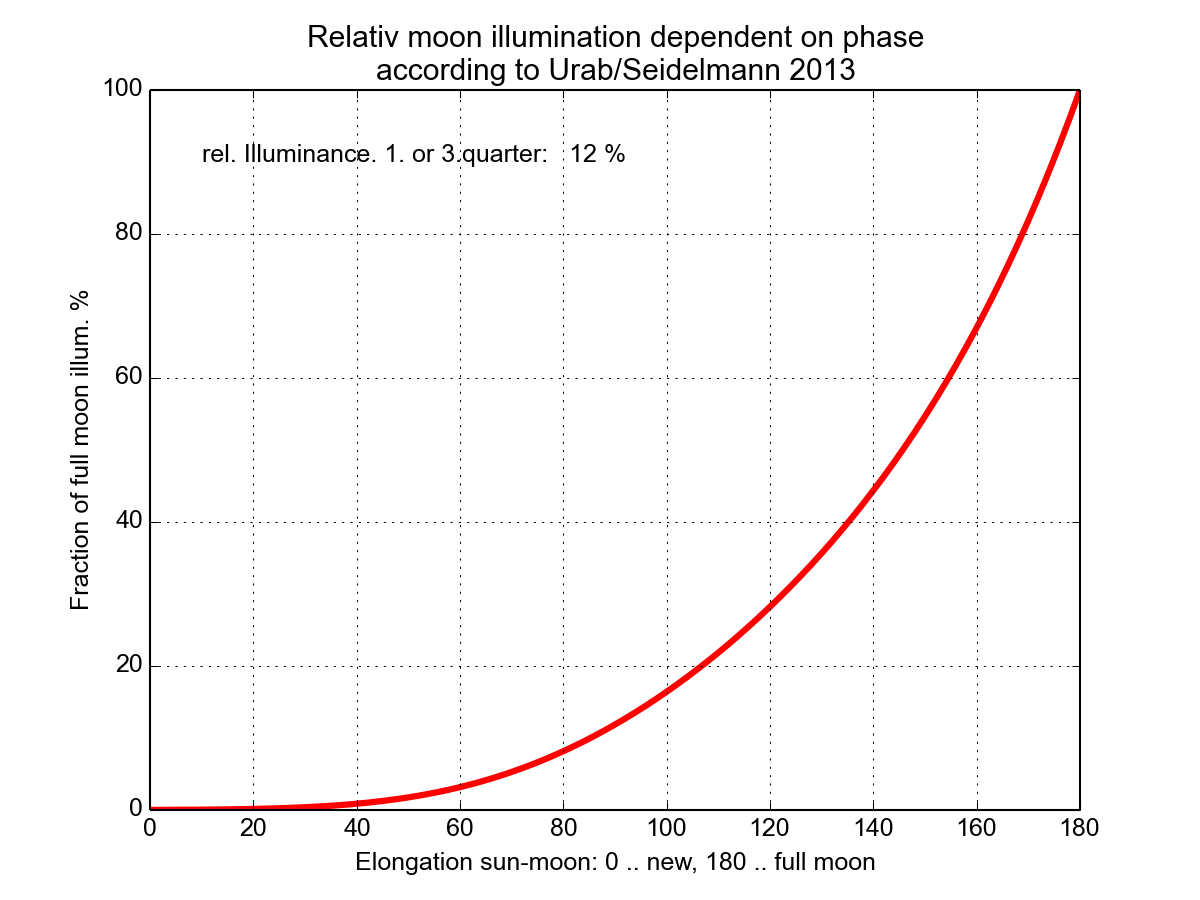
5.3.2. Relative Moon Illuminance¶

The relative illuminance is defined as the ratio of 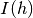$I(h)$ with the (il)luminance of the mean moon at the zenith 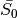$\bar{S_0}$ :

$\mathrm{rel.Ill.} = \frac{I(h)}{\bar{S_0}}$

See the program code in module adnite2.constants for the actual value of the mean maximum moon illuminace. It should be somewhere about 265 mlx.

5.3.3. Twilight Illuminance¶

Because day time illuminances are not of interest quite a simple approach can be used:

$S(h) = S_0 + (S_0 - S_{-\infty}) e^{b h} b = \ln{(S_H - S_{-\infty})/(S_0 - S_{-\infty})}$

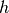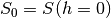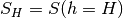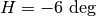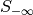with $h$ the sun altitude, $S_0 = S(h=0)$ , $S_H = S(h=H)$ , e.g. $H = -6 \; \mathrm{deg}$ (ECET) as extra value, and $S_{-\infty}$ as the deep night background value (star light plus air glow).

See module code adnite2.constants or in the configfile adnite2.cfg for the actual values taken.

5.3.4. The Cloud Equation¶

According to the master thesis Hur mörkt blir det (How bright is it) by Lena Nilsson at the University of Uppsala (2007) the cloudiness effect on surface illumination can be approximated by a multiple bulk scattering process. Nilsson presents an equation that is derived from the sum of downward AND upward radiation. We think that is not justified. Downward radiation at the ground is all we need.

A further improvement can be applied by taking into account clear sky backscattering. This can be achieved by using a sort of clear sky atmospheric albedo 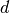$d$ as in Möller (1965).

The total amount of available light below clouds is given by (see Thaler (2015)):

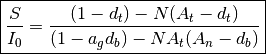
$\boxed{\frac{S}{I_0} = \frac{(1-d_t) - N(A_t - d_t)}{(1-a_g d_b) - N A_t (A_n - d_b)}}$

with:

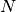$N$ … amount of clouds (0 .. 1)
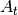$A_{t}$ … albedo of cloud tops
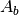$A_{b}$ … albedo of cloud base
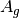$A_{g}$ … surface albedo
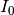$I_0$ … incident radiation at top of the clouds
$S$ … available light below the clouds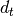
$d_t$ … backscattering albedo of the clear sky atmosphere for the incoming radiation (“top” of atmosphere)
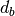$d_b$ … backscattering albedo of the clear sky atmosphere for the ground radiation (“bottom” of atmosphere).

Albedo values

Rough estimates derived form Möller (1965) and Nielsson (2007). Any dependence of the direction of the incoming radiation is neglected.

Remark	Value
Cloud top
NS	0.90
SC	0.70
ST or thin SC	0.65
Cloud bottom
NS	0.90
SC	0.70
ST	0.65
thin ST or SC	0.50
thick AC or AS	0.70
CS	0.35
CI (or haze)	0.20
Ground
sea without waves	0.20
sea with moderate to high waves	0.04
ice without snow	0.55
ice with fresh snow	0.80
dense forest, no snow	0.05
dense forest, dry snow	0.50
wet ground	0.05
humid ground	0.10
dry ground	0.20
snow slush	0.35
dry fresh snow	0.70
old snow, half covering	0.25
desert	0.25
Atmospheric albedo (Möller, 1965)
Rayleigh atmosphere	0.07
medium turbid atmosphere	0.15
highly turbid atmosphere	0.25

5.3.5. Sources¶

Fritz Möller: On the backscattering of global radiation by the sky. Tellus XVII (1965), 3 (Retrieved Aug. 2015)

Lena Nilsson: Hur mörkt blir det? Institutionen för geovetenskaper, Uppsala Universitet, Juni 2007. (Retrieved March 2016). Available as an internal German translation.

D. Thaler (2015): Multiple scattering of incomming short wave radiation between clouds and ground. (Retrieved March 2016)

S.E. Urban, P.K. Seidelmann (edit.): Explanatory supplement to the Astronomical Almanac. 3rd edition. University science Books (Mill valley, California, 2013)

Footnotes

[1]	USNO data services cannot be reached via an Austrian IP-adress. Use an US proxy server instead.